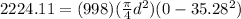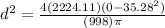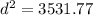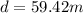Question

A horizontal water jet at 70˚F issues from a circular orifice in a large tank. The jet strikes a vertical plate that is normal to the axis of the jet. A force of 500 lbf is needed to hold the plate in place against the action of the jet. If the pressure in the tank is 90 psig at point A, what is the diameter D of the jet just downstream of the orifice?

Answer 1

In order to solve this problem, it is necessary to take into account the concepts related to Bernoulli's equation and the propulsive force.

Bernoulli's equation is defined by,

`(P_A)/(\rho g)+(V_A^2)/(2g) +z_a = (P_B)/(\rho g)+(V_B^2)/(2g) +z_B`

Where

P = Pressure

v = velocity

z= Heigth

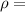`\rho =`Density

g = Gravitational Force

We must look for the speed at the exit. Our values are given by,

`V_A = 0`

`P_A = 90Psi=620528Pa`

`T = 70\°F = 21.11\°C`

`\rho = 998kg/m^3`

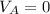
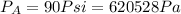
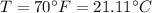
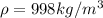
Since water is exposed to atmosphere outlet at the end, then
`P_B = 0`

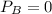
Replacing we have

`(P_A)/(\rho g)+(V_A^2)/(2g) +z_a = (P_B)/(\rho g)+(V_B^2)/(2g) +z_B`

`(620528)/(998(9.8))+(0^2)/(2(9.8)) +0 = (0)/(998(9.81))+(V_B^2)/(2(9.81)) +0`

`63.4460 = (V_B^2)/(2(9.81))`

`V_B = √(2(63.4460)(9.81))`

`V_B = 35.28m/s`

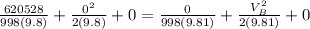
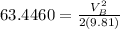
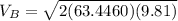
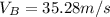
According to the statement, the required force is given by 500Lbf that is 2224.11N

Based on the propulsive force we have to

`F_x = \rho A(V_C+V_B)`

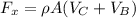
Replacing our values,

`2224.11 = (998)((\pi)/(4)d^2)(0-35.28^2)`

`d^2=(4(2224.11)(0-35.28^2))/((998)\pi)`

`d^2 = 3531.77`

`d = 59.42m`