Question

A group of students perform the same "Conservation of Mechanical Energy" experiment that you performed in lab by allowing a solid sphere and then a solid cylinder to roll down the ramp. Both objects were released from the same position at the top of the ramp. If the speed vsphere of the solid sphere at the bottom of the ramp was 1.45 m/s, what would be the speed vcylinder at the bottom of the ramp

Answer 1

v'=1.4 m/s

Step-by-step explanation:

Lets take mass and the radius for cylinder and sphere is same.

Mass = m

Radius = r

Moment of inertia of sphere I

`I=(2)/(5)mr^2`

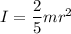
Moment of inertia of cylinder I'

`I'=(1)/(2)mr^2`

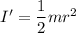
Lets take height of ramp = h

Energy conservation for sphere

`mgh=(1)/(2)mv^2+(1)/(2)I\omega ^2`

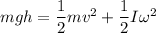
If we take as motion is pure rolling with out slipping then

v= ωr

`mgh=(1)/(2)mv^2+(1)/(2)I\left((v)/(r)\right)^2` ---1

Energy conservation for cylinder

`mgh=(1)/(2)mv'^2+(1)/(2)I'\omega' ^2`

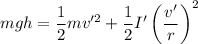`mgh=(1)/(2)mv'^2+(1)/(2)I'\left((v')/(r)\right)^2` ---2

From equation 1 and 2

`(1)/(2)mv^2+(1)/(2)I\left((v)/(r)\right)^2=(1)/(2)mv'^2+(1)/(2)I'\left((v')/(r)\right)^2`

`mv^2+I\left((v)/(r)\right)^2=mv'^2+I'\left((v')/(r)\right)^2`

`mv^2+(2)/(5)mr^2\left((v)/(r)\right)^2=mv'^2+(1)/(2)mr^2\left((v')/(r)\right)^2`

`mv^2+(2)/(5)mv^2=mv'^2+(1)/(2)mv'^2`

`v^2+(2)/(5)v^2=v'^2+(1)/(2)v'^2`

`(7)/(5)v^2=(3)/(2)v'^2`

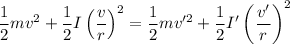
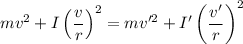
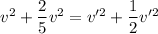
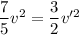
1.4 x 1.45²= 1.5 x v'²

v'=1.4 m/s

This is the speed of cylinder at the bottom.