Question

A 73 Kg wagon is being pulled by a 210 Newton force that is 25 degrees above horizontal on the right. The coefficient of friction on this wagon is 0.23. *There is no net force in the Y direction, watch your Fn. What is the acceleration?

Answer 1

Acceleration of a wagon is
`1.973 \mathrm{m} / \mathrm{s}^(2)`

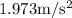
Step-by-step explanation:

From the given question,

Coefficient of friction (µ) = 0.23

Mass of the wagon (m) = 73kg

We know that

Force of friction = µN

µ is coefficient of friction which are given 0.23

N is the normal reaction

Weight (w) = mg. (Applies at all times even when the object is not accelerated)

g on the earth surface =
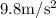`9.8 \mathrm{m} / \mathrm{s}^(2)`, substitute the mass and acceleration due to gravity of the earth to obtain Weight.

`W=73 \mathrm{kg} * 9.8 \mathrm{m} / \mathrm{s}^(2)`

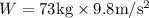
W = 715.4N

We came to know that the wagon is not moving on vertical direction and no net force in Y direction hence this follows:

`\text { Force}{*} \sin 25+N=\text { weight }`

Force = 210 N

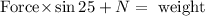
`210 * 0.422+\mathrm{N}=715.4 \mathrm{N}`

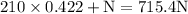
88.74 + N = 715

N = 715 - 88.74

N = 626.26

Force of friction = µN

Force of friction =
`0.23 * 626.26`

Force of friction = 144.04N

To find the acceleration of a wagon. We know that F = ma

`\text {acceleration }(a)=(F)/(m)`

`\text {acceleration }(a)=\frac{144.04 \mathrm{N}}{73}`

`\text {acceleration }(a)=1.973 \mathrm{m} / \mathrm{s}^(2)`

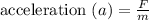
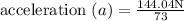
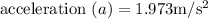
Therefore acceleration of a wagon is
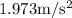`1.973 \mathrm{m} / \mathrm{s}^(2)`.