Question

When a truckload of apples arrives at a packing plant, a random sample of 150 is selected and examined for bruises, discoloration, and other defects.

The whole truckload will be rejected if more than 5% of the sample is unsatisfactory.
Suppose that in fact 8% of the apples on the truck do not meet the desired standard.

What's the probability that the shipment will be accepted anyway?
a. 0.0222
b. 0.9778
c. 0.088
d. 0.912

Answer 1

c. 0.088

Explanation:

Let p(s) be the proportion of apples defected in the sample. The probability that p(s)<0.05 can be calculated by calculating z statistic of 0.05:

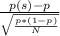`\frac{p(s)-p}{\sqrt{(p*(1-p))/(N) } }` where

• p(s) = 0.05

• p is the proportion of the apples in fact defected (0.08)

• N is the sample size (150) Then,

z(0.05)=
`\frac{0.05-0.08}{\sqrt{(0.08*0.92))/(150) } }=-1.354`

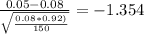
And P(z<-1.354)≈0.0879

Therefore the probability that a random sample of 150 among 8% defected apples can be accepted is 0.088.