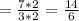Question

there are 3 dogs at the pound and 7 cats which could be an equivalent ratios of cats to dogs from amir​

Answer 1

An equivalent ratio could be:
`(14)/(6)`

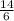
Explanation:

By definition, ratios are used to compare two or more quantities.

In this case we are comparing the number of cats and the number of dogs at the pound.

According to the information given in the exercise, there are 3 dogs and 7 cats, so we can write the following ratio of cats to dogs:

`(Number\ of\ cats)/(Number\ of\ dogs)=(7)/(3)`

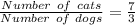
In order to find an equivalent ratio, we can multiply the numerator and the denominator by the same amount. Let's multiply them by 2.

So, an equivalent ratio could be:

`=(7*2)/(3*2)=(14)/(6)`