Answer: 0.0668
Explanation:
Given : The population of lengths of aluminum-coated steel sheets is normally distributed with a mean of 30.05 inches and a standard deviation of 0.2 inches.
i.e.
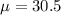 and
and
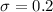
Let x denotes the lengths of aluminum-coated steel sheets.
Then the probability that a randomly selected sample of 4 sheets will have an average length of less than 29.9 inches long will be :-
![P(x<29.9)=P((x-\mu)/((\sigma)/(√(n)))<(29.9-30.05)/((0.2)/(√(4))))\\\\=P(z<-1.5)=1-P(z<1.5)\ \ [\because\ P(Z<-z)=1-P(Z<z)]](https://img.qammunity.org/2020/formulas/mathematics/college/jkj4b3g3tjh11fd5v1zyvksij66k9avn4f.png)
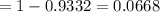 [by using the z-value table ]
[by using the z-value table ]
Hence, the required probability = 0.0668