Answer: a. N(0.92, 0.0215)
Explanation:
For population proportion (p) and sample size n, the mean and standard deviation is given by :-
The sampling distribution model for p is given by :_

, where
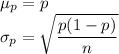
We assume that the seeds are randomly selected.
Given : Information on a packet of seeds claims that the germination rate is 92%.
i.e. p= 0.92
The packet contains 160 seeds.
i.e. n= 160
Then ,

Hence, the sampling distribution model for p is:
