Question

A(n) 1610 kg car is moving along a level road at 21.7 m/s. The driver accelerates, and in the next 10 s the engine provides 22100 J of additional energy. If 3683.33 J of this energy must be used to overcome friction, what is the final speed of the car? Answer in units of m/s.

Answer 1

v=22.22 m/s

Step-by-step explanation:

Given that

m= 1610 kg

initial velocity ,u= 21.7 m/s

The energy provided by engine(W₁) = 22100 J

The energy lost in the friction(W₂) = 3683.33 J

Lets take final velocity of the car = v m/s

Now from energy conservation

Work done by all forces = Change in the kinetic energy

W₁ + W₂ = ΔKE

`W_1 - W_2=(1)/(2)mv^2-(1)/(2)mu^2`

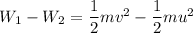
By putting the values

`W_1 - W_2=(1)/(2)mv^2-(1)/(2)mu^2`

`22100 - 3683.33=(1)/(2)* 1610 v^2-(1)/(2)* 1610 * 21.7^2`

`(1)/(2)* 1610 v^2=22100 - 3683.33+(1)/(2)* 1610 * 21.7^2`

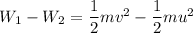
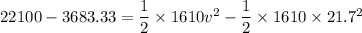
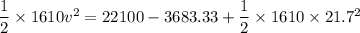
v=22.22 m/s

This is final speed of the car.