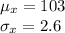Answer:
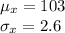
Explanation:
For any random variable x,
We know that the mean and the standard deviation of the sampling distribution of the sample mean x is given by :-
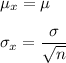
, where n = sample size.
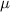 = population mean
= population mean
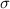 = population standard deviation equal.
= population standard deviation equal.
Given : n=25
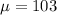
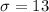
Then , the mean and the standard deviation of the sampling distribution of the sample mean x will be :-
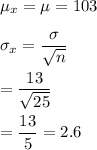
Hence, the mean and the standard deviation of the sampling distribution of the sample mean x :