Question

The logarithm of x, written log(x), tells you the power to which you would raise 10 to get x. So, if y=log(x), then x=10^y. It is easy to take the logarithm of a number such as 10^2, because you can directly see what power 10 is raised to. That is, log(10^2)=2. What is the value of log(1,000,000)?

Answer 1

To solve this problem it is necessary to apply the rules and concepts related to logarithmic operations.

From the definition of logarithm we know that,

`Log_(10)(10) = 1`

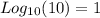
In this way for the given example we have that a logarithm with base 10 expressed in the problem can be represented as,

`log_(10)(1,000,000)`

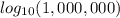
We can express this also as,

`log_(10)(10^6)`

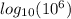
By properties of the logarithms we know that the logarithm of a power of a number is equal to the product between the exponent of the power and the logarithm of the number.

So this can be expressed as

`6*log_(10)(10)`

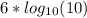
Since the definition of the base logarithm 10 of 10 is equal to 1 then

`6*1=6`

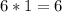
The value of the given logarithm is equal to 6