Question

A circle is growing so that the radius is increasing at the rate of 3 cm/min. How fast is the area of the circle changing at the instant the radius is 12 cm? Include units in your answer.

Answer 1

The area is growing at a rate of
`(dA)/(dt) =226.2 \,(cm^2)/(min)`

Explanation:

Notice that this problem requires the use of implicit differentiation in related rates (some some calculus concepts to be understood), and not all middle school students cover such.

We identify that the info given on the increasing rate of the circle's radius is 3
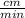`(cm)/(min)` and we identify such as the following differential rate:

`(dr)/(dt) = 3\,(cm)/(min)`

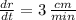
Our unknown is the rate at which the area (A) of the circle is growing under these circumstances,that is, we need to find
`(dA)/(dt)`.

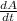So we look into a formula for the area (A) of a circle in terms of its radius (r), so as to have a way of connecting both quantities (A and r):

`A=\pi\,r^2`

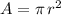
We now apply the derivative operator with respect to time (
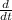`(d)/(dt)`) to this equation, and use chain rule as we find the quadratic form of the radius:

`(d)/(dt) [A=\pi\,r^2]\\(dA)/(dt) =\pi\,*2*r*(dr)/(dt)`

Now we replace the known values of the rate at which the radius is growing (
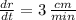`(dr)/(dt) = 3\,(cm)/(min)`), and also the value of the radius (r = 12 cm) at which we need to find he specific rate of change for the area :

`(dA)/(dt) =\pi\,*2*r*(dr)/(dt)\\(dA)/(dt) =\pi\,*2*(12\,cm)*(3\,(cm)/(min)) \\(dA)/(dt) =226.19467 \,(cm^2)/(min)\\`

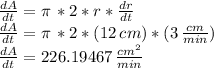
which we can round to one decimal place as:

`(dA)/(dt) =226.2 \,(cm^2)/(min)`