Question

A random sample of 16 students selected from the student body of a large university had an average age of 25 years and a standard deviation of 2 years. We want to determine if the average age of all the students at the university is significantly more than 24. Assume the distribution of the population of ages is normal. The test statistic is a. 1.96. b. 2.00. c. .05. d. 1.65.

Answer 1

Answer: Option 'b' is correct.

Explanation:

Since we have given that

Average age = 25 years

Standard deviation = 2 years

Sample size = 16

So, Null hypothesis :
`H_0:\mu\leq 24`

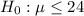
Alternate hypothesis:
`H_1:\mu>24`

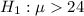
Level of significance = 5% = 0.05

So, test statistic would be

`\frac{\bar{X}-\mu}{(\sigma)/(√(n))}\\\\=(25-24)/((2)/(√(16)))\\\\=(1)/((2)/(4))}\\\\=(1)/(0.5)\\\\=2`

Hence, Option 'b' is correct.