Question

(33%) Problem 3: Two cars collide at an icy intersection and stick together afterward. The first car has a mass of 1100 kg and is approaching at 8.5 m/s due south. The second car has a mass of 650 kg and is approaching at 17.5 m/s due west.

Answer 1

The final velocity of the cars is 8.38 m/s at an angle 39.1° south of west.

Step-by-step explanation:

Given that,

Mass of first car = 1100 kg

Velocity of first car = 8.5 m/s

Mass of second car = 650 kg

Velocity of second car = 17.5 m/s

Suppose we need to find the final velocity of the cars and direction of the cars.

We need to calculate the velocity of the car in west direction

Using conservation of momentum in west direction

`m_(f)v_(f)+m_(s)v_(s)= (m_(f)+m_(s))v_(x)`

`v_(x)=(m_(f)v_(f)+m_(s)v_(s))/((m_(f)+m_(s)))`

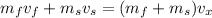
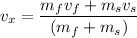
Put the value into the formula

`v_(x)=(1100*0+650*17.5)/(1100+650)`

`v_(x)=6.5\ m/s`

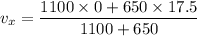
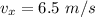
We need to calculate the velocity of the car in south direction

Using conservation of momentum in south direction

`m_(f)v_(f)+m_(s)v_(s)= (m_(f)+m_(s))v_(y)`

`v_(y)=(m_(f)v_(f)+m_(s)v_(s))/((m_(f)+m_(s)))`

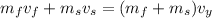
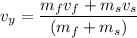
Put the value into the formula

`v_(y)=(1100*8.5+650*0)/(1100+650)`

`v_(y)=5.3\ m/s`

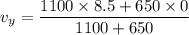
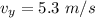
We need to calculate the final velocity of the cars

Using formula of velocity

`v_(eq)=√((6.5)^2+(5.3)^2)`

`v_(eq)=8.38\ m/s`

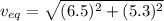
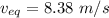
We need to calculate the direction

Using formula of direction

`\tan\theta=(v_(y))/(v_(x))`

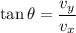
Put the value into the formula

`\tan\theta=(5.3)/(6.5)`

`\theta=\tan^(-1)((5.3)/(6.5))`

`\theta=39.1^(\circ)`

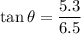
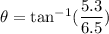
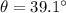
Hence, The final velocity of the cars is 8.38 m/s at an angle 39.1° south of west.