Question

In a grandfather clock, the second hand moves forward by one second for each half period of the clock’s pendulum.

a. How long would you expect the pendulum to be in a grandfather clock?
b. If you took a grandfather clock to the moon, where gravity is 1/6 Earth’s gravity, what would you expect to happen to the period of the clock?
c. What happens to the apparent passage of time on the moon?

Answer 1

To solve the problem it is necessary to take into account the concepts related to simple pendulum, i.e., a point mass that is suspended from a weightless string. Such a pendulum moves in a harmonic motion -the oscillations repeat regularly, and kineticenergy is transformed into potntial energy and vice versa.

In the given problem half of the period is equivalent to 1 second so the pendulum period is,

`T= 2s`

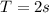
From the equations describing the period of a simple pendulum you have to

`T = 2\pi \sqrt{(L)/(g)}`

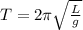
Where

g= gravity

L = Length

T = Period

Re-arrange to find L we have

`L = (gT^2)/(4\pi^2)`

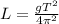
Replacing the values,

`L = ((9.8)(2)^2)/(4\pi^2)`

`L = 0.99m`

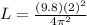
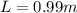
In the case of the reduction of gravity because the pendulum is in another celestial body, as the moon for example would happen that,

`T = 2\pi \sqrt{(L)/(g/6)}`

`T = 2\pi\sqrt{(6L)/(g)}`

`T = 2\pi \sqrt{(6*0.99)/(9.8)}`

`T  = 4.89s`

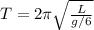
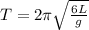
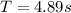
In this way preserving the same length of the rope but decreasing the gravity the Period would increase considerably.