Question

After coming down a slope, a 60-kg skier is coasting northward on a level, snowy surface at a constant 15 m>s. Her 5.0-kg cat, initially running southward at 3.8 m>s, leaps into her arms, and she catches it. (a) Determine the amount of kinetic energy converted to internal energy in the Earth reference frame. (b) What is the velocity, measured in the Earth reference frame, of an inertial reference frame in which the cat’s kinetic energy does not change?

Answer 1

To solve this exercise, it is necessary to apply the concepts of conservation of the moment especially in objects that experience an inelastic colposition.

They are expressed as,

`m_1v_1+m_2v_2 = (m_1+m_2)v_f`

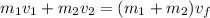
Where,

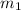`m_1`= mass of the skier

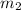`m_2`= mass of the cat

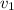`v_1` = initial velocity of skier

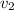`v_2` = initial velocity of cat

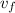`v_f`= final velocity of both

Re-arrange to find V_f we have,

`V_f = (m_1v_1+m_2v_2)/((m_1+m_2))`

`V_f = ((60)(15)+(5)(-3.8))/((60+5))`

`V_f = 13.55m/s`

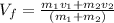
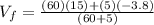
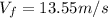
Once the final velocity is found it is possible to calculate the change in kinetic energy, so

`\Delta KE = KE_i-KE_f`

`\Delta KE = (1)/(2)(m_1v_1^2+m_2v^2_2)-(1)/(2)(m_1+m_2)v_f^2`

`\Delta KE = (1)/(2)((60)(15)^2+(5)(-3.8)^2)-(1)/(2)(60+5)(13.55)^2`

`\Delta KE = 819.1J`

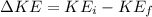
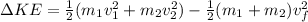
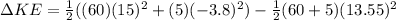
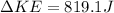
Therefore the amount of kinetic energy converted in to internal energy is 819J