Question

A sample that is 2 cm thick is inserted into one arm of a Michelson interferometer that was adjusted to give a maximum reading. The maximum is reestablished when the mirror is pushed 1.9 cm closer to the beamsplitter. What is the index of refraction of the sample?

Answer 1

1.95

Step-by-step explanation:

r = Thickness of sample = 2 cm

x = Displacement = 1.9 cm

`\mu` = Refractive index of sample

The Michelson interferometer is an interferometer that uses arms which are split into two light sources.

Constructive interference is given by

`l=m\lambda`

Destructive interference is given by

`l=(m+0.5)\lamda`

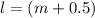
where,

m = 1, 2, 3.....

`\lambda` = Wavelength

In a Michelson Interferometer experiment, thickness is given by

`t=(x)/(\mu-1)\\\Rightarrow \mu-1=(x)/(t)\\\Rightarrow \mu=(x)/(t)+1\\\Rightarrow \mu=(1.9)/(2)+1\\\Rightarrow \mu=1.95`

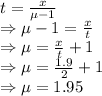
The refractive index of the sample is 1.95

Answer 2

μ = 1.95

Step-by-step explanation:

Given that

thickness ,t= 2 cm

Displacement ,x= 1.9 cm

Now from Michelson interferometer ,the relationship between index of refraction , thickness and the displacement given as

`t=(x)/(\mu -1)`

Now by putting the values

`t=(x)/(\mu -1)`

`2=(1.9)/(\mu -1)`

μ-1 = 0.95

μ = 1+ 0.95

μ = 1.95

So the index of refraction μ will be 1.95.