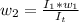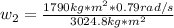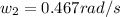Question

A 4.2-m-diameter merry-go-round is rotating freely with an angular velocity of 0.79 rad/s . Its total moment of inertia is 1790 kg⋅m2 . Four people standing on the ground, each of mass 70 kg , suddenly step onto the edge of the merry-go-round.

Answer 1

`w_2=0.467rad/s`

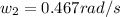
Step-by-step explanation:

Four people standing on the ground each of mass and usually this questions have to find the final angular velocity

`m_t=4*70kg=280kg`

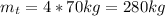
The radius
`r=4.2/2=2.1m`

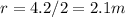
Angular velocity
`w_1=0.79rad/s`

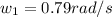
The moment of inertia total is
`I_t=1790 kg/m^2`

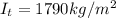
Momento if inertia

`I_1=m_t*r^2`

`I_1=280kg*(2.1m)^2=1234.8kg*m^2`

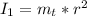
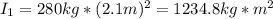
Angular momentum

`I_1*w_1=I_t*w_2`

Solve to w2

`w_2=(I_1*w_1)/(I_t)`

`w_2=(1790kg*m^2*0.79rad/s)/(3024.8kg*m^2)`

`w_2=0.467rad/s`