Answer: 0.0170
Explanation:
Given : The mean amount purchased by a typical customer at Churchill’s Grocery Store is $23.50, with a standard deviation of $5.00.
i.e.
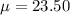
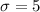
We assume the distribution of amounts purchased follows the normal distribution.
Sample size : n=50
Let
 be the sample mean.
be the sample mean.
Formula :
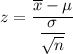
Then, the probability that the sample mean is at least $25.00 will be :-

Hence, the likelihood the sample mean is at least $25.00= 0.0170