Answer:
The height is 24.03 cm.
Step-by-step explanation:
Given that,
Mass = 1.60 kg
Force constant = 200 N/m
Mass of metal ball = 285 g
Distance x= 14.8 cm
Suppose How high above point A will the tray be when the metal ball leaves the tray?
The force exerted by the spring in the downward
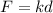 ...(I)
...(I)
The downward force is
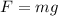 ...(II)
...(II)
From equation (I) and (II)
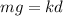
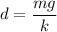
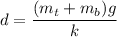
Put the value into the formula
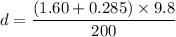
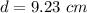
The point here is 9.23 cm above the equilibrium point and therefore the high above point A is
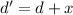
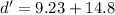
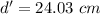
Hence, The height is 24.03 cm.