Question

An engineer is going to redesign an ejection seat for an airplane. The seat was designed for pilots weighing between 130 lb and 171 lb. The new population of pilots has normally distributed weights with a mean of 136 lb and a standard deviation of 28.1 lb. a. If a pilot is randomly​ selected, find the probability that his weight is between 130 lb and 171 lb.

Answer 1

0.4757

Explanation:

Mean =
`\mu = 136 lb`

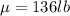
Standard deviation =
`\sigma = 28.1 lb`

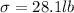
We are supposed to find If a pilot is randomly​ selected, find the probability that his weight is between 130 lb and 171 lb i.e.P(130<x<171)

Formula:
`Z=(x-\mu)/(\sigma)`

`Z=(x-\mu)/(\sigma)`

at x = 130

`Z=(130-136)/(28.1)`

`Z=-0.213`

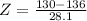
Refer the z table of p value

P(x<130)=0.4168

`Z=(x-\mu)/(\sigma)`

at x = 171

`Z=(171-136)/(28.1)`

`Z=1.245`

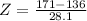
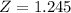
Refer the z table of p value

P(x<171)=0.8925

P(P(130<x<171)=P(x<171)-P(x<130)= 0.8925-0.4168=0.4757

Hence the probability that his weight is between 130 lb and 171 lb is 0.4757