Question

If the specific surface energy for aluminum oxide is 0.90 J/m2 and its modulus of elasticity is (393 GPa), compute the critical stress required for the propagation of an internal crack of length 0.6 mm. ___ MPa

Answer 1

critical stress required for the propagation is 27.396615 ×
`10^(6)` N/m²

Step-by-step explanation:

given data

specific surface energy = 0.90 J/m²

modulus of elasticity E = 393 GPa = 393 ×
`10^(9)` N/m²

internal crack length = 0.6 mm

to find out

critical stress required for the propagation

solution

we will apply here critical stress formula for propagation of internal crack

( σc ) =
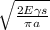`\sqrt{(2E\gamma s)/(\pi a)}` .....................1

here E is modulus of elasticity and γs is specific surface energy and a is half length of crack i.e 0.3 mm = 0.3 ×
`10^(-3)` m

so now put value in equation 1 we get

( σc ) =
`\sqrt{(2E\gamma s)/(\pi a)}`

( σc ) =
`\sqrt{(2*393*10^9*0.90)/(\pi 0.3*10^(-3))}`

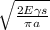
( σc ) = 27.396615 ×
`10^(6)` N/m²

so critical stress required for the propagation is 27.396615 ×
`10^(6)` N/m²