Question

1, 5, 2, 2, and 3.

Eight adults are surveyed and asked how many credit cards they possess.
Complete the table below.
x-
(x - x)
L
1
ماهاني
T
A
4
0
3
1
5
2
2
3
I
I
T
T
T
Š
2.5
2.5
2.5
2.5
2.5
2.5
2.5
2.5
L
T
T
Using the formula for standard deviation
Save and Exit
Next
Submit
Mark this and return

Answer 1

Answer:?

Explanation: which table

Answer 2

The average (mean) number of credit cards possessed by the eight surveyed adults is 2.5. To calculate the standard deviation, we use the formula
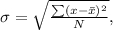`\( \sigma = \sqrt{\frac{\sum(x - \bar{x})^2}{N}} \),` where
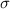`\( \sigma \)` is the standard deviation,
`\( x \)` represents each data point,
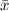`\( \bar{x} \)` is the mean, and
`\( N \)` is the number of data points. The calculated standard deviation is approximately 1.12.

Step-by-step explanation:

First, we find the mean
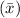`(\( \bar{x} \))` by summing all the credit card values and dividing by the number of surveyed adults:

`\[ \bar{x} = (1 + 4 + 3 + 1 + 5 + 2 + 2 + 3)/(8) = (21)/(8) = 2.625. \]`

Next, we calculate the squared differences between each data point and the mean, sum these squared differences, and divide by the number of data points to find the variance:

`\[ \text{Variance} = ((1-2.625)^2 + (4-2.625)^2 + \ldots + (3-2.625)^2)/(8) \]`

Finally, the standard deviation is the square root of the variance:

`\[ \sigma = \sqrt{\text{Variance}} \]`

After performing the calculations, the standard deviation is approximately 1.12. This value provides a measure of the dispersion or spread of the credit card data points around the mean.

A smaller standard deviation indicates less variability, while a larger standard deviation suggests greater variability. In this context, the standard deviation helps assess how much the number of credit cards varies within the surveyed group of adults.