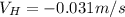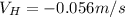Answer:
a)
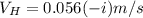
b)
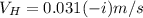
Step-by-step explanation:
By conservation of the linear momentum:
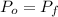
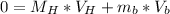
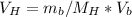
When the bullet is shot horizontally
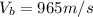
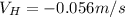
When the bullet is shot at 56.0° above the horizontal,
![V_b = 965*[cos(56),sin(56)]m/s=[539.62;800.02]m/s](https://img.qammunity.org/2020/formulas/physics/college/dhcnps72wustbxi7zxi34uz439yw8abtb6.png)
Since on the y-axis ground will absorb the shock, we only make the calculations on the x-axis: