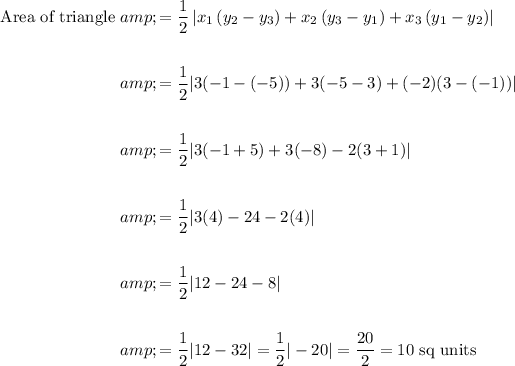Question

What is the area of a triangle whose vertices are D(3, 3) , E(3, −1) , and F(−2, −5) ?

Enter your answer in the box.

units²

Answer 1

The area of the triangle is 10 sq units

SOLUTION:

Given, we have to find the area of a triangle whose vertices are D(3, 3), E(3, −1) and F(−2, −5)

We know that,

`\text { Area of triangle }=(1)/(2)\left[x_(1)\left(y_(2)-y_(3)\right)+x_(2)\left(y_(3)-y_(1)\right)+x_(3)\left(y_(1)-y_(2)\right)\right]`

Where,
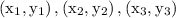`\left(\mathrm{x}_(1), \mathrm{y}_(1)\right),\left(\mathrm{x}_(2), \mathrm{y}_(2)\right),\left(\mathrm{x}_(3), \mathrm{y}_(3)\right)` are vertices of the triangle.

Here in our problem,
`\left(\mathrm{x}_(1), \mathrm{y}_(1)\right)=(3,3),\left(\mathrm{x}_(2), \mathrm{y}_(2)\right)=(3,-1) \text { and }\left(\mathrm{x}_(3), \mathrm{y}_(3)\right)=(-2,-5)`

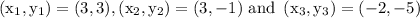
Now, substitute the above values in the formula.

`\begin{aligned} \text { Area of triangle } &=(1)/(2)\left|x_(1)\left(y_(2)-y_(3)\right)+x_(2)\left(y_(3)-y_(1)\right)+x_(3)\left(y_(1)-y_(2)\right)\right| \\\\ &=(1)/(2)|3(-1-(-5))+3(-5-3)+(-2)(3-(-1))| \\\\ &=(1)/(2)|3(-1+5)+3(-8)-2(3+1)| \\\\ &=(1)/(2)|3(4)-24-2(4)| \\\\ &=(1)/(2)|12-24-8| \\\\ &=(1)/(2)|12-32|=(1)/(2)|-20|=(20)/(2)=10 \text { sq units } \end{aligned}`