Answer:
The ball will be at 100 feet at time x=0.5 sec and at time x=7.5 sec
Explanation:
The correct question is
A ball is launched upward from a height 40 feet above ground level. the ball's height at t seconds is given by h(t)=-16t^2+128t+40 At what time(s) will the ball be at 100 feet?
we have
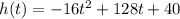
so
For h(t)=100 ft
substitute in the equation and solve for x

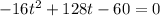
The formula to solve a quadratic equation of the form

is equal to

in this problem we have
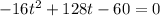
so
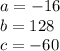
substitute in the formula
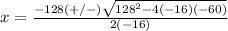

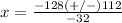
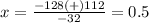
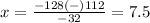
therefore
The ball will be at 100 feet at time x=0.5 sec and at time x=7.5 sec