Answer: B. 1.679
Explanation:
The standard deviation of the difference between the two means is given by :-
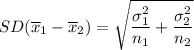
If true population standard deviations are not available , then
we estimate the standard error as
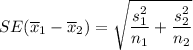
Given :
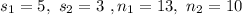
Then , the standard deviation of the difference between the two means will be :-
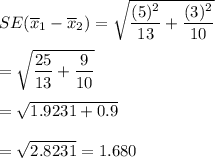
Hence, the correct answer is B. 1.679