Answer:
 represents a particular any term and
represents a particular any term and
 represents just previous term.
represents just previous term.
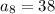
Explanation:
In the given recursive formula,
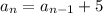
 represents
represents
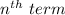
and
 represents just its previous term.
represents just its previous term.
To find
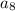 , first five terms are given there. We need to find its previous terms
, first five terms are given there. We need to find its previous terms

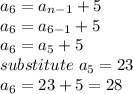
Similarly,
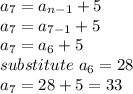
Similarly,
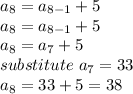
Thus
 is the answer.
is the answer.