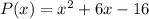Answer:
Standard form of polynomial with zeros 2 and -8 is
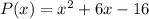
Explanation:
Here, the zeroes of the polynomial P(x) is given as x = 2 and x = -3
If x = a is a zero pf the polynomial p(x) , then (x-a) is the root of the given polynomial.
⇒ (x- 2) and (x -(-8)) are the two roots of the polynomial P(x).
Now, Polynomial P(x) = Product of all its Roots
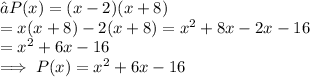
Hence the standard form of polynomial with zeros 2 and -8 is