Answer:
901 flies
Explanation:
Let the total population of flies is P,
While
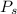 and
and
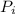 represent the number of flies that survived and that are initially respectively.
represent the number of flies that survived and that are initially respectively.
Here,
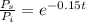

Differentiating w. r. t. t ( time ),
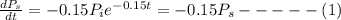
Now, if 6 flies are added per hour,
Then the number of flies added per day = 24 × 6 = 144 ( ∵ 1 day = 24 hours),
So,

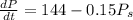
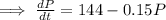
When P =
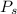 =
=
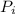
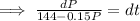
∵ if t = 0, P = 400,
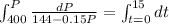
![[(\ln(144-0.15P))/(-0.15)}]_(400)^(P) = [t]_(0)^(15)](https://img.qammunity.org/2020/formulas/mathematics/college/6vljs9predzhqnoz9nrltj2si491azq35v.png)
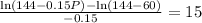
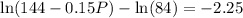
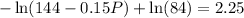
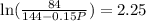
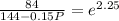
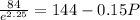
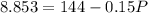

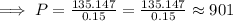
i.e. 901 flies would present.