Answer: 0.9987
Explanation:
Given : The weights of newborn babies are distributed normally, with a mean of approximately 105 oz and a standard deviation of 10 oz.
i.e.
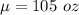 and
and
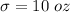
Let x represents the weights of newborn babies.
If a newborn baby is selected at random, then the probability that the baby weighs more than 75 oz will be :-
![P(x>75)=P((x-\mu)/(\sigma)>(75-105)/(10))\\\\ =P(z>-3 )=P(z<3)\ \ \ [\because\ P(Z>-z)=P(Z<z)]](https://img.qammunity.org/2020/formulas/mathematics/high-school/tr1dkdwm6lc2n5bsoz15rhv77vvch5pttq.png)
 [using z-value table]
[using z-value table]
Hence, the required probability = 0.9987