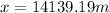Answer: 14139.19 m
Step-by-step explanation:
This situation is related to parabolic motion and can be solved using the following equations:
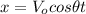 (1)
(1)
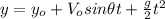 (2)
(2)
Where:
 is the horizontal distance (where the artillery shell lands)
is the horizontal distance (where the artillery shell lands)
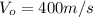 is the initial velocity
is the initial velocity
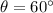 is the angle
is the angle
 is the time
is the time
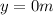 is the final height
is the final height
 is the initial height
is the initial height
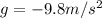 is the acceleration due gravity, always directed downwards
is the acceleration due gravity, always directed downwards
So, let's begin by isolating
 from (2):
from (2):
 (3)
(3)
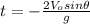 (4)
(4)
Substituting (4) in (1):
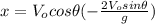 (5)
(5)
Rewriting (5) and taking into account
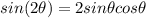 :
:
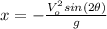 (6)
(6)
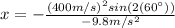 (7)
(7)
Finally: