Answer:
Option C)
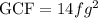
Explanation:
We are given the following:
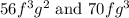
We have to find the greatest common factor of the two expressions.
We will use the technique of prime factorization to do so:

The common factors of both expressions are:
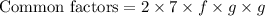
Thus, the greatest common factor is:
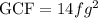
Option C) is the correct option.