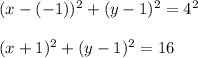Answer:
Last option:
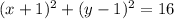
Explanation:
The missing figure is attached.
The center-radius form of the circle equation is:
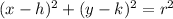
Where the center of the circle is at the poitn
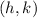 and "r" is the radius.
and "r" is the radius.
You can identify from the figure attached that the radius of the circle shown is 4 units.
Since the other circle has the same radius and its center is at the point
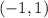 ; you can identify that:
; you can identify that:
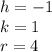
Therefore, substituting values into
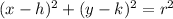 , you get that the equation of that circle is:
, you get that the equation of that circle is: