Answer:
The distance between the points A and B is 49 meters.
Explanation:
Here we have to use "The law of sines" and find distance between the points A and B.
Law of sines =

Where a, b, c are the sides of a triangle and A, B, and C are the angles of the triangle.
First let's draw the figure of the given situation.
From the given information, we can form a triangle ABC.
We are given two angles. We can find the third angle ABC
The sum of the three angles add upto 180 degrees.
78.33 + 34.167 + ∠ABC = 180
112.497 + ∠ABC = 180
∠ABC = 180 - 112.497
∠ABC = 67.503°
So, ∠A = 78.33° , ∠B = 67.503° and ∠C = 34.167°
We know that side AC = b = 81.3 m
Now we can use the law of sine and find the length AB.
In the triangle, AB is called the side c which is opposite to the angle C.
AC is called the side b which is opposite to the angle B.
\frac{b}{sin B} = \frac{c}{sin C}[/tex]
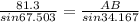
Now we can find the value of sin 67.503 and sin 34.167 using the calculator, we get
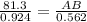
Cross multiplying, we get
0.924 × AB = 81.3 × 0.562
AB = 45.6906 ÷ 0.924
AB = 49.45 meters
When we round off to nearest meters, we get
AB = 49 meters.
Therefore, the distance between the points A and B is 49 meters.