Question

Group points {(0,1),(0,5)(2,6),(3,3)}is not a function, but group points {(1,4)(2,7)(3,1)(5,7)} is a function. What do you notice about two groups of point? What makes it a function?

Answer 1

Any value in the domain of the function should have a unique value in codomain.

Explanation:

In the first set of points
`\{`
`\text{(0,1),(0,5)(2,6),(3,3)}`
`\}`,

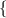
value
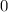`0` maps to two distinct values
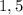`1,5` in the codomain.

This violates the property of functions.

The first set of points does not form a function.

In the second set of points
`\{`
`\text{(1,4),(2,7)(3,1),(5,7)}`
`\}`,

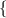
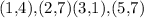
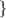Every value in domain corresponds to unique value in domain.

There is no violation in the property of functions.

The second set of points does form a function.