Answer:
The area of triangle for the given coordinates is 1.5
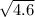
Explanation:
Given coordinates of triangles as
A = (0,0)
B = (3,4)
C = (3,2)
So, The measure of length AB = a =
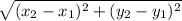
Or, a =
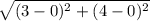
Or, a =
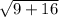
Or, a =
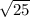
∴ a = 5 unit
Similarly
The measure of length BC = b =
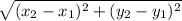
Or, b =
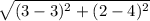
Or, a =
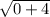
Or, b =
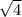
∴ b = 2 unit
And
So, The measure of length CA = c =
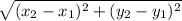
Or, c =

Or, c =
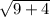
Or, c =
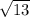
∴ c =
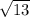 unit
unit
Now, area of Triangle written as , from Heron's formula
A =
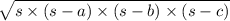
and s =
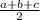
I.e s =

Or. s =
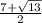
So, A =

Or, A =
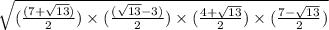
Or, A =
 ×
×
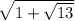
∴ Area of triangle = 1.5
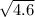
Hence The area of triangle for the given coordinates is 1.5
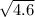 Answer
Answer