Question

On a coordinate plane, triangle A B C has points (1, 1), (4, 0), (3, 5).What is the area of triangle ABC?

Answer 1

Area of Triangle ABC =
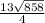`(13√(858) )/(4)` unit² or 7.32 unit²

Explanation:

Given coordinates of Triangle are

A = ( 1 , 1)

B = ( 4 , 0)

C = ( 3 , 5)

So , The measure of side AB is

AB =
`\sqrt{(x_2-x_1)^(2)+(y_2-y_1)^(2)}`

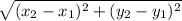
or, AB =
`\sqrt{(4-1)^(2)+(0-1)^(2)}`

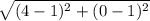
Or, AB =
`\sqrt{(3)^(2)+(-1)^(2)}`

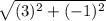
∴ AB =
`√(10)`

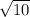
Again ,

The measure of side BC is

BC =
`\sqrt{(x_2-x_1)^(2)+(y_2-y_1)^(2)}`

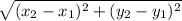
or, BC =
`\sqrt{(3-4)^(2)+(5-0)^(2)}`

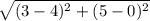
Or, BC =
`\sqrt{(-1)^(2)+(5)^(2)}`

∴ BC =
`√(26)`

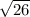
Similarly ,

The measure of side CA is

CA =
`\sqrt{(x_2-x_1)^(2)+(y_2-y_1)^(2)}`

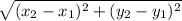
or, CA =
`\sqrt{(3-1)^(2)+(5-1)^(2)}`

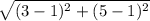
Or, CA =
`\sqrt{(2)^(2)+(4)^(2)}`

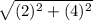
∴ CA =
`√(20)`

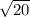
Now, let D be the mid points of side BC

So, Points ( D ) =
`((x_1+x_2))/(2)` ,
`((y_1+y_2))/(2)`

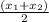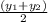
I.e points d =
`((4+3))/(2)` ,
`((0+5))/(2)`

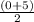
Or, points D =
`((7))/(2)` ,
`((5))/(2)`

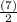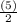
Now Measure of line AD is

AD =
`\sqrt{(x_2-x_1)^(2)+(y_2-y_1)^(2)}`

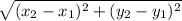
AD =
`(\sqrt{(7)/(2)-1})^(2)` +
`(\sqrt{(5)/(2)-1})^(2)`

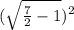Or, AD =(
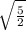`\sqrt{(5)/(2) }` )² + (
`\sqrt{(3)/(2) }` )²

Or, AD =
`\sqrt{(33)/(4) }`

Now, Area of Triangle ABC =
`(1)/(2)` × length × base

or, Area of Triangle ABC =
`(1)/(2)` × AD × BC

or, Area of Triangle ABC =
`(1)/(2)` ×
`\sqrt{(33)/(4) }` ×
`√(26)`

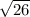
Or, Area of Triangle ABC =
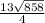`(13√(858) )/(4)` unit² or , 7.32 unit² Answer

Answer 2

7 square units.

Explanation:

On the coordinate plane, triangle ABC has vertices at (1,1), (4,0) and (3,5).

So, the area of the triangle ABC is given by

`(1)/(2) | 1(0 - 5) + 4(5 - 1) + 3(1 - 0) | = 7` square units. (Answer)

We know the formula that area of triangle having vertices at
`(x_(1), y_(1))`,
`(x_(2), y_(2))`, and
`(x_(3), y_(3))` is given by

Δ =
`(1)/(2) | x_(1)(y_(2) - y_(3)) + x_(2)(y_(3) - y_(1)) + x_(3)(y_(1) - y_(2))|`