Question

Suppose of barium acetate is dissolved in of a aqueous solution of ammonium sulfate. Calculate the final molarity of barium cation in the solution. You can assume the volume of the solution doesn't change when the barium acetate is dissolved in it. Be sure your answer has the correct number of significant digits.

Answer 1

To calculate the final molarity of barium cation in the solution, multiply the molarity of Ba²+ ions by the volume, and then divide the moles by the final solution volume. The final molarity of barium cation in the solution is 1.7 × 10^-3 M.

Step-by-step explanation:

To calculate the final molarity of barium cation in the solution, we need to consider the ion product—Q = [Ba²+][SO4²¯]—using the concentrations of the ions that are present after the solutions are mixed and before any reaction occurs. First, calculate the moles of Ba²+ by multiplying the molarity (0.0050 M) by the volume in liters (0.010 L), which gives 5.0 × 10^-5 mol Ba²+. Then, calculate the concentration of Ba²+ by dividing the moles by the final solution volume of 0.030 L. The final molarity of barium cation in the solution is 1.7 × 10^-3 M.

Answer 2

Step-by-step explanation:

Let us assume that the given data is as follows.

mass of barium acetate = 2.19 g

volume = 150 ml = 0.150 L (as 1 L = 1000 ml)

concentration of the aqueous solution = 0.10 M

Therefore, the reaction equation will be as follows.

`Ba(C_(2)H_(3)O_(2))_(2) \rightarrow Ba^(2+) + 2C_(2)H_(3)O^(-)_(2)`

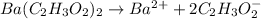
Hence, moles of
`C_(2)H_(3)O^(-)_(2)` =
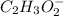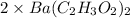`2 * Ba(C_(2)H_(3)O_(2))_(2)` .......... (1)

As, No. of moles =
`\frac{mass}{\text{molar mass}}`

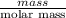
Hence, moles of
`Ba(C_(2)H_(3)O_(2))_(2)` will be calculated as follows.

No. of moles =
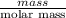
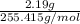`\frac{mass}{\text{molar mass}}`

=
`(2.19 g)/(255.415 g/mol)` (molar mass of
`Ba(C_(2)H_(3)O_(2))_(2)` is 255.415 g/mol)

=
`8.57 * 10^(-3)`

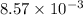
Moles of
`C_(2)H_(3)O^(-)_(2)` =
`2 * 8.57 * 10^(-3)`

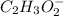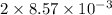
= 0.01715 mol

Hence, final molarity will be as follows.

Molarity =
`\frac{\text{no. of moles}}{volume}`

=
`(0.01715 mol)/(0.150 L)`

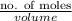
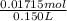
= 0.114 M

Thus, we can conclude that final molarity of barium cation in the solution is 0.114 M.