Question

A 40.0-mL solution contains 0.019 M barium chloride (BaCl2). What is the minimum concentration of sodium sulfate (Na2SO4) required in the solution to produce a barium sulfate (BaSO4) precipitate? The solubility product for barium sulfate is Ksp = 1.1 ✕ 10−10.

Answer 1

The minimum concentration of sodium sulfate required to producer precipitation is
`5.790* 10^(-9) M`.

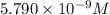Step-by-step explanation:

`BaCl_2\rightarrwo Ba^(2+)+2Cl^-`

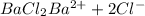
Concentration of barium chloride=
`[BaCl_2]=0.019 M`

Concentration of barium ions =
`[Ba^(2+)]`

1 mol of barium chloride gives 1 mol of barium ions.

`[Ba^(2+)]=[BaCl_2]=0.019 M`

The solubility product for barium sulfate=
`K_(sp) = 1.1* 10^(-10)`

`BaSO_4\rightleftharpoons Ba^(2+)+SO_4^(2-)`

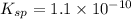
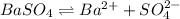
0.019 M S

The expression of solubility product for barium sulfate:

`K_(sp)=[Ba^(2+)]* S`

`K_(sp)=0.019 M* S`

`S=(1.1* 10^(-10))/(0.019 M)=5.790* 10^(-9) M`

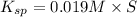
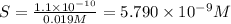
The minimum concentration of sulfate ions =
`[SO_4^(2-)]=5.790* 10^(-9) M`

`Na_2SO_4(aq)\rightarrow 2Na^+(aq)+SO_4^(2-)(aq)`

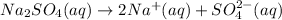
1 mole of sulfate ions are proceed form 1 mole of sodium sulfate solution.

Then
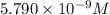`5.790* 10^(-9) M` sulfate ions will be obtained from:

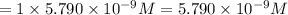`=1* 5.790* 10^(-9) M=5.790* 10^(-9) M` of sodium sulfate

The minimum concentration of sodium sulfate required to producer precipitation is
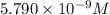`5.790* 10^(-9) M`.