Question

Suppose the function P(t) = 437.6(1.031)t is used to model the population of an organism in a specific region after t years. When will the number of organisms be 1000? (Round your answer to three decimal places.)

Answer 1

Answer: 27.071 years.

Explanation:

The given function :
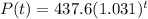`P(t) = 437.6(1.031)^t` is used to model the population of an organism in a specific region after t years.

To find : t , when P(t)=1000

Substitute P(t)=1000 in the given function , we get

`1000 = 437.6(1.031)^t\\\\\Rightarrow\ (1000)/(437.6)=(1.031)^t\\\\\Rightarrow\ 2.2852=(1.031)^t`

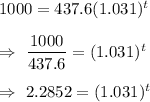
Taking natural log on both sides , we get

`\ln(2.2852)=\ln ((1.031)^t)\\\\\Rightarrow\ \ln(2.2852)=t(\ln (1.031))\\\\\Rightarrow\ t=( \ln(2.2852)/(\ln(1.031))\\\\\Rightarrow\ t=(0.8264535)/(0.0305292)\\\\\Rightarrow\ t=27.070918989\approx27.071`

Hence, The number of organisms will be 1000 after t= 27.071 years.