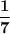Answer:
Explanation:
The probability density function for x which is uniformally distributed in interval [a,b] is given by :-
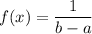
Given : The times required for a cable company to fix cable problems in its customers' homes are uniformly distributed between 13 minutes and 20 minutes.
Then,
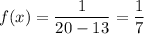
Now, the probability that a randomly selected cable repair visit will take at least 19 minutes will be :_
![\int^(20)_(19)\ f(x)\ dx\\\\=\int^(20)_(19)((1)/(7))\ dx\\\\= (1)/(7)[x]^(20)_(19)\\\\=(1)/(7)[20-19]=(1)/(7)](https://img.qammunity.org/2020/formulas/mathematics/college/kpelkemxkydwr8qyeeqp5jfvichahm9p6u.png)
Hence, the probability that a randomly selected cable repair visit will take at least 19 minutes =