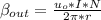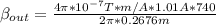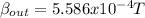Answer:
a.
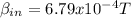
b.
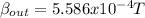
Step-by-step explanation:
Given:
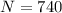 ,
,
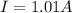 ,
,
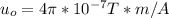 .
.
The magnetic field can be find using the Gauss law in the equation of field magnetic at the inner radius and the outer radius knowing the inner radius and the outer radius are:
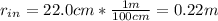
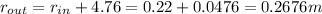
a.
Magnetic field inner
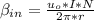

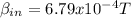
b.
Magnetic field outer