Question

Gerald needs to purchase baseballs and bats for his youth baseball league. He'll need at least 25 pieces of equipment, but he only has $615 to spend. Baseballs cost $20 each and bats cost $35 each. Which is a combination of baseballs and bats that Gerald can afford to buy?

Answer 1

D: (29, 1)

Explanation:

I got the choices for the given problem as:

A: (22, 3)

B: (22, 5)

C: (24, 1)

D: (29, 1)

Let x represent number of baseballs and y represent number of bats.

We have been given that Gerald will need at least 25 pieces of equipment. We can represent this information in an inequality as:

`x+y\geq 25...(1)`

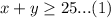
Baseballs cost $20 each, so cost of x baseballs would be
`20x`.

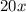Bats cost $35 each, so cost of y bats would be
`35y`.

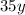We are also told that Gerald has only $615 to spend. We can represent this information in an equation as:

`20x+35y\leq 615...(2)`

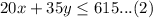
Upon checking the given ordered pairs in our both inequalities, we can see that each ordered pair is a solution for our system of inequalities.

1st pair represents 25 pieces of equipment, 2nd pair represents 27 pieces of equipment and 3rd pair represents 25 pieces of equipment

Since ordered pair (29,1) represents 30 pieces of equipment, which is largest, therefore, option D is the correct choice.