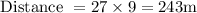Question

A giant blue diamond is thrown off a cliff with an initial horizontal velocity of 27.0 m/s. The

cliff is 413.8 meters high. How far from the base of the cliff does the diamond fall?

Answer 1

The diamond will fall 243 m far from the base of the cliff.

Explanation:

As the diamond is thrown off the cliff, the diamond will follow a projectile path with free fall. So the velocity component will be splitted as horizontal and vertical velocity. The horizontal component of velocity will remain constant as given at 27 m/s but the vertical velocity will be varying at the rate of 9.8 m/s as the diamond will be reaching the ground due to free fall.

So gravity will act upon the diamond leading to exhibit acceleration due to gravity will falling. Thus with the help of second equation of motion, we can determine the time taken by the diamond to reach the ground from a height of 413.8 m.

As the second equation of motion is

`s=u t+(1)/(2) a t^(2)`

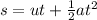
As the initial velocity of the diamond before thrown is zero, u = 0 and as the diamond is exhibiting a free fall, so acceleration a will be equal to acceleration due to gravity g. And the displacement performed by the diamond will be equal to the height of the cliff.

Thus,

`413.8=(0 * t)+\left((1)/(2) * g * t^(2)\right)`

`413.8=\left((1)/(2) * 9.8 * t^(2)\right)`

`t^(2)=(413.8 * 2)/(9.8)=84.44`

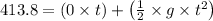
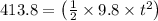
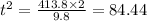
Thus, the time taken for crossing the cliff is t = 9 s.

Now the distance at which the diamond falls far from the base of the cliff can be found as

Thus,

`\text { Distance }=27 * 9=243 \mathrm{m}`