Answer:
x = 1 is a local maxima
Explanation:
Let us start by finding the first and second derivatives of this function
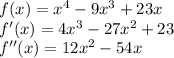
Now let's find the value of the second derivative at x=1.
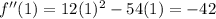
So the second derivative is negative which means that there is a local maxima at x = 1