Question

Helppppp Maricella plots two ordered pairs on the grid below.

-


No 0000


(8.67


(6,2)-


1 2


3


4


5


6


7 8


9


x


The line segment is extended to cross both axes. What is the location of the y-intercept on the line?


(0, -22)


(0-10)


(0.-5)


Mark this and return


Save and Exit


Next


Submit

Answer 1

B (0,-10)

Explanation:

Answer 2

Option 2, i.e., (0,-10)

Explanation:

Consider the below figure is attached with this question.

If a line passes through two points
`(x_1,y_1)` and
`(x_2,y_2)`, then the equation of line is

`y-y_1=(y_2-y_1)/(x_2-x_1)(x-x_1)`

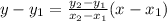
From the below graph it is clear that the line passes through the point (8,6) and (6,2).

`y-6=(2-6)/(6-8)(x-8)`

`y-6=2(x-8)`

`y-6=2x-16`

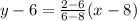
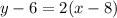
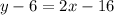
Add 6 on both sides.

`y=2x-10`

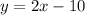
Substitute x=0 to find the y-intercept of the line.

`y=2(0)-10`

`y=-10`

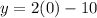
The location of the y-intercept on the line is (0,-10). Therefore, the correct option is 2.