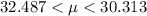Question

Here are summary statistics for randomly selected weights of newborn​ girls: n=185​,

x bar = 31.4 ​hg, s=7.5 hg. Construct a confidence interval estimate of the mean. Use a 95​% confidence level.


What is the confidence interval for the population mean μ​?

Answer 1

The confidence interval for the population mean μ​ is
`32.487<\mu <30.313`

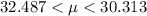
Explanation:

Given :

Number of weights of newborn​ girls n=185.

Mean
`\bar{x}=31.4` hg

Standard deviation s=7.5 hg

Use a 95​% confidence level i.e. cl=0.95

To find : What is the confidence interval for the population mean μ​?

Solution :

Using t-distribution,

The degree of freedom
`DF=n-1=185-1=184`

`\alpha=(1-0.95)/(2)`

`\alpha=0.025`

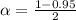
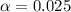
The t critical value is t=1.973.

The confidence interval build is

`CI=\bar{x}\pm(t\cdot (s)/(√(n)))`

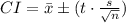
Substitute the values,

`CI=31.4\pm(1.973\cdot (7.5)/(√(185)))`

`CI=31.4\pm(1.973\cdot 0.5514)`

`CI=31.4\pm(1.087)`

`31.4+1.087<\mu <31.4-1.087`

`32.487<\mu<30.313`

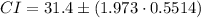
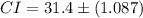
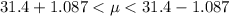
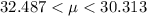
Therefore, the confidence interval for the population mean μ​ is
`32.487<\mu <30.313`