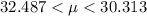Answer:
The confidence interval for the population mean μ is
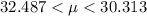
Explanation:
Given :
Number of weights of newborn girls n=185.
Mean
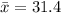 hg
hg
Standard deviation s=7.5 hg
Use a 95% confidence level i.e. cl=0.95
To find : What is the confidence interval for the population mean μ?
Solution :
Using t-distribution,
The degree of freedom
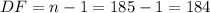
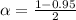
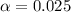
The t critical value is t=1.973.
The confidence interval build is
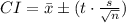
Substitute the values,
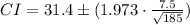
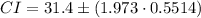
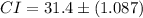
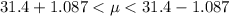
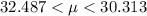
Therefore, the confidence interval for the population mean μ is