Answer:
Option 2.
Explanation:
We need to find a function g(x) which has x-intercepts at (1/2,0) and (6,0).
To find the x-intercepts substitute g(x)=0 in function.
For option 1,
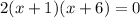
Using zero product property we get
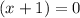 and
and

 and
and

Therefore the x-intercepts of this function at (-1,0) and (-6,0).
For option 2,
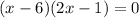
Using zero product property we get
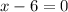 and
and
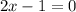
 and
and
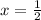
Therefore the x-intercepts of this function at (1/2,0) and (6,0).
For option 3,
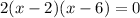
Using zero product property we get
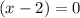 and
and

 and
and

Therefore the x-intercepts of this function at (2,0) and (6,0).
For option 4,

Using zero product property we get
 and
and
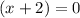
 and
and

Therefore the x-intercepts of this function at (-2,0) and (-6,0).
Therefore, the correct option is 2.