Question

One number is 2 more than another. The difference between their squares is 24.

Answer 1

Answer: x = 7; y = 5

Explanation:

Let's call the first number x and the second number y so we can form a system in which:

x - y = 2

x² - y² = 24

isolating x from the first equation:

x = 2 + y

replacing x that is worth 2 + y in the second equation

(2 + y)² - y² = 24

4 + 2 . 2 . y + y² - y² = 24

4 + 4y = 24

4y = 24 - 4

4y = 24

y = 20/4

y = 5

substituting the y that is worth 5 in the first equation:

x - y = 2

x - 5 = 2

x = 2 + 5

x = 7

I hope this help

Answer 2

Answer: The numbers are 7 and 5

Explanation:

Let the first number be x and the second number be y.

From the first statement , it was said that one of the number is two more than the other , that is

x - y = 2 .................. equation 1

square of x is
`x^(2)` and the square of y is
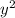`y^(2)` , the difference between thier squares implies

`x^(2)` -
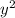`y^(2)` = 24 .............. equation 2

solving the resulting simultaneous equations by substitution method:

From equation 1 , make x the subject of the formula , that is

x = 2 + y ............. equation 3

substitute equation 3 into equation 2 , we have

`(2+y)^(2)` -
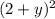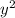`y^(2)` = 24

Expanding , we have

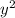`y^(2)` + 4y + 4 -
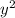`y^(2)` = 24

4y + 4 = 24

Subtract 4 from both sides

4y = 20

y = 20/4

y = 5

substitute y = 5 into equation 3 , we have

x = 5+ 2

x = 7

Therefor the numbers are 7 and 5